목차
1. 쿨롱의 법칙
2. 쿨롱의 법칙에서 도출된 전기장의 크기
3. 쿨롱의 법칙으로 전기장의 가우스 법칙 유도
*참고하면 좋은 내용

맥스웰 방정식은 물리학의 기초가 되는 중요한 방정식이며,
그렇기 때문에 한번에 확 등장한 식이 아니다.
많은 사람들의 실험들과 수식들이 하나로
정립되어 맥스웰 방정식이 발표됐다.
그렇다면, 맥스웰 방정식의 시작은 무엇이었을까.
전기장의 가우스 법칙은 쿨롱의 법칙에서부터 시작했다.
1. 쿨롱의 법칙

쿨롱의 법칙은
'전하를 띠고 있는 입자 사이에는 전기력이라는 힘이 존재한다.'
는 것이다.
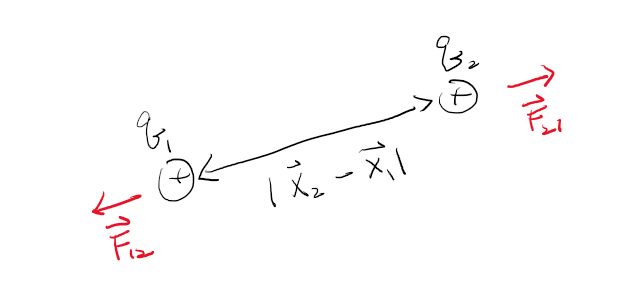
이때, X는 두 입자의 위치 벡터를 나타대며,
F21 은 X2이 X1에 가해주는 힘을 의미한다.
q는 각각의 전하를 의미하며,
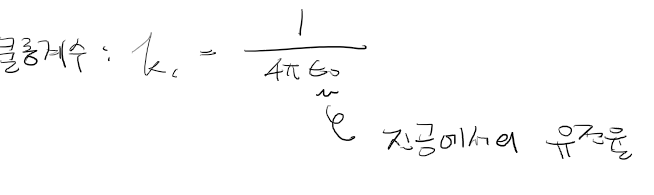
쿨롱 계수 kc의 크기는 위와 같다.
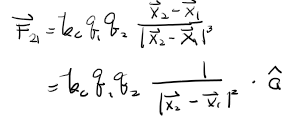
식 1은 방향벡터 a 를 사용하여 식 2처럼 나타낼 수 있으며,
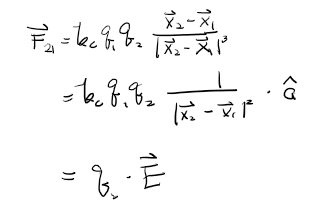
이는 다시 식 3으로 나타낼 수 있다.
2. 쿨롱의 법칙에서 도출된 전기장의 크기
식 3에서 E 는 전기장을 나타낸다.
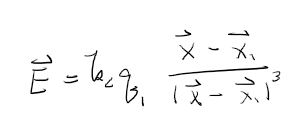
따라서, 전기장은 위의 식으로 나타난다.

여기서 X2가 아니라 X로 사용한 이유는
전기장이 단지 두개의 원자와 원사 사이에 작용하는 힘이 아니라
모든 위치로부터 작용하는 힘이기 때문이다.

따라서, 각 전하로부터의 합으로 표현이 가능하다.
위의 식은 점전하들이 이산적으로 분포된 경우이다.
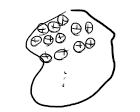
실제로는 이산적으로 분포돼 있기보다는
도체에서처럼 균일하면서도 촘촘하게 분포돼 있는 경우가 많다.
따라서, 적분의 형태로 식을 표현한다.
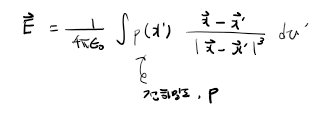

즉, 전기장은 위의 그림에서처럼
X'의 부피가 X라는 점에 미치는 전체 영향이다.
3. 쿨롱의 법칙으로 전기장의 가우스 법칙 유도
점전하 주변으로 임의의 가상의 구(부피)를 만들어서
쿨롱의 법칙으로 가우스 법칙을 유도할 수 있다.
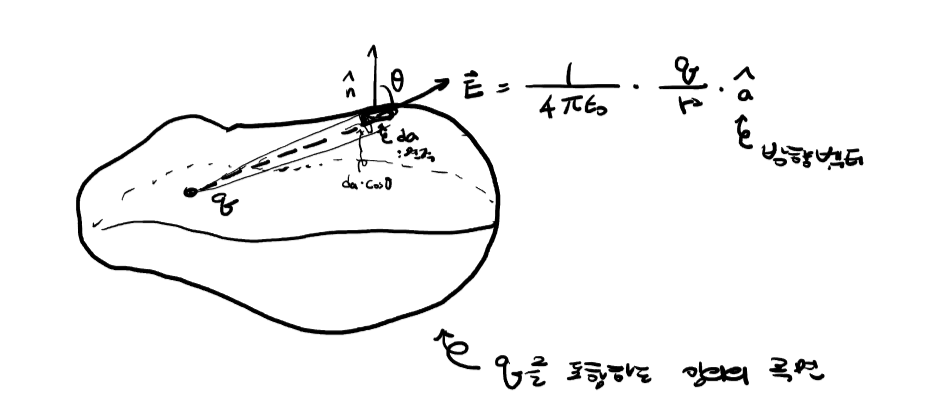
그림처럼 점전하 q 를 둘러싼 임의의 곡선(부피)가 있을 때,
미소면적에 점전하 q 가 미치는 전기장의 크기는
아래의 식 6처럼 표현이 가능하다.
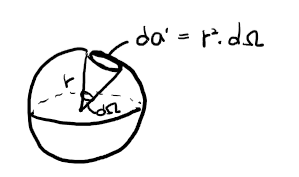
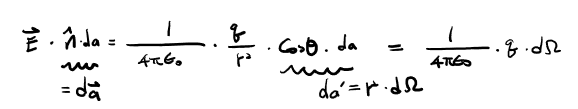
이 식에 적분을 취하면, 아래의 식 7이 되고,
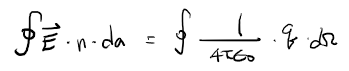
여기서 단위 원으로 상정하면 식 8을 얻을 수 있다.

이때, n 은 미소면적 a의 법선벡터를 나타내며,
따라서 식 9, 전기장의 가우스 법칙 적분형태를 얻을 수 있다.
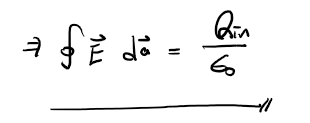
'물리학 이모저모' 카테고리의 다른 글
| 스넬의 굴절 법칙 간단한 유도 방법 (3) | 2021.04.25 |
|---|---|
| 전파의 속도 : 위상속도 vs 군속도( + 분산) (2) | 2021.04.25 |
| 광학의 분류 (0) | 2021.04.24 |
| 맥스웰 방정식의 적분형/미분형, 각 방정식의 의미 (1) | 2021.02.14 |
| 복소수 기초 (0) | 2021.01.28 |



